
扫码添加微信,获取更多半导体相关资料
引言
本文考虑了相互作用的2个数量级范围,以考虑了实际粒子的形状和材料,将这些相互作用与静电电荷、阻力、表面张力、冲击波、高加速度和气溶胶粒子所产生的排斥力进行相互比较,可以预测不同清洗过程的内在能力和局限性。已经确定了三种颗粒去除过程——能够去除所有颗粒尺寸和类型的通用过程,甚至来自图案晶片,具有相同理论能力但实际上受到粒子可及性的限制,最后是无法去除所有颗粒尺寸的清洗。
通过计算施加给细颗粒的主要力,在表中可以看出驱动粒子粘附/去除机制的四个主要参数是静电、范德华、毛细管和阻力。表面张力γlg是由于介质分子之间的内聚力,并倾向于使界面区域最小化,它代表每单位界面长度的一个力,对于参考球形粒子,当液体完美地润湿颗粒材料,气体/液体界面作用于整个粒子周长时,得到最大的毛细力(见图1):

图1 作用于液体/气体界面的粒子的最大毛细管力示意图
运动流体的粘度会对粒子产生阻力,在直径为D的球形粒子放置在流速Vp中的情况下,用斯托克斯定律给出了一个很好的近似,直到雷诺数为101,其中,µ表示流体粘度:20◦C下的水为10−3kg/m/s,这种力理论上只能将粒子平行于表面。可以预期,粒子上或衬底上的粗糙度将使这种切向力转化为发射动量,在非球形粒子的情况下,阻力通常较高。
本文研究了作用于参考刚性粒子和球形粒子的范德华引力与实际粒子之间的区别,实际粒子的非理想性的结果:扁平化、非特定形状、粗糙度、部分嵌入等,最终可以看作是与基底接触的附加平面,理想球与刚性球与实际非理想粒子的差值任意用等于接触表面的分数f除以同维粒子能够呈现πR2的最大表面表示,结果如图所示2,粒径为10~150纳米。可以看出,范德瓦尔斯力随粒子的非理想性而迅速增加,并且可以比理想粒子高出2个数量级以上,这种效应随着粒径的增大而减小。
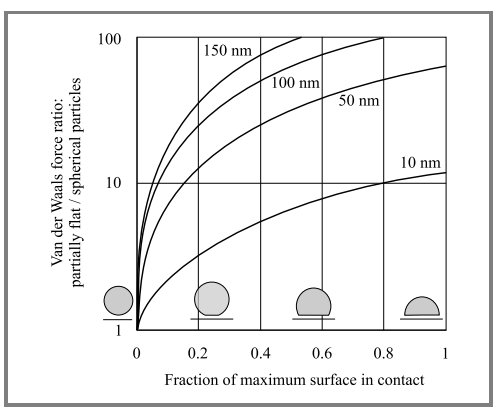
图2
扩散层的厚度是由于施加在带电表面形成的反离子上的静电吸引和它们在本体溶液中的再扩散之间的竞争造成的,因此,高温和低离子强度可以了扩散层厚度。在图5显示了Si和二氧化硅作为衬底材料和最正电粒子材料之一-氧化铝的Zeta电位相对于pH的演变。
为了便于粒子去除和防止任何再沉积,希望在所有粒子类型和衬底上收集的电荷具有相同的符号,从而导致静电斥力。在A和B区域都满足这个条件。
颗粒去除机制
本文讨论了常规和前瞻性颗粒清洗过程的理论性能。这种清洗机制包括通过消耗基底、粒子或两者都将粒子与基底分离,直到静电产生的排斥力超过范德瓦尔斯力,这意味着pH必须在A或B区域进行调整,静电力随距离的减小速度慢于范德华相互作用,因此,无论粒子的大小和电荷如何,释放距离始终存在。这种理论蚀刻厚度在实践中通过去除过程的动态行为而增加。事实上,在分离开始时,由于范德瓦尔斯相互作用,蚀刻速度和粒子的再吸引速度之间发生了竞争。
晶片导致了一个非常高的速度的非均匀射流,生成的液滴以400m/s的速度投射到衬底上。计算表明,当碰撞时,液滴的前部甚至以大约600m/s[13]的速度加速和撞击粒子,与连续射流不同,这里施加的力是由液滴前部施加于粒子表面的激波产生的。当温度为3000k,压力为1000atm时,气泡坍塌过程中释放的能量密度是相当大的,气泡越大,势释放能越高。当气泡靠近表面坍塌时,它会诱导液体微射流向表面,达到每秒数百米的极高速度。这种喷射流会产生非常强烈的局部激波。通过超声发光,在高达850kHz的超大气体范围内观察到声空化。然而,我们不可能得出这样的结论:由于产生较小气泡而产生的激波也是由同样的射流现象引起的。如图所示11,声浴中产生的周期性压力波变化倾向于增加。
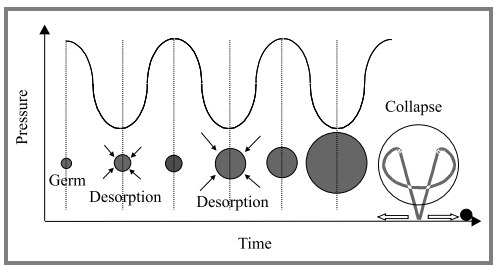
图11 在超声波激发下气泡大小的演化 直到坍塌
在实践中,加速度受到可接受的硅通量的限制,导致硅熔化,这个阈值在实验中对应于去除大约100纳米的第一个氧化铝颗粒(乐观的情况),用方程计算出相应的加速度,在106g范围内,为了提高激光清洗的去除能力,首先将薄层液体从蒸汽浓缩到基底上,在这项工作中,覆盖2个数量级的范德华相互作用被认为考虑了实际形状和材料的大多数粒子。这个范围是通过考虑来确定的。哈默克常数的可能变化,以及理想刚性球与具有有限接触面积的实粒子之间的差值、扁平效应等。
不同的粒子去除过程可以根据所使用的物理效应进行分类,如静电、阻力和毛细管力、冲击波、加速度或动能。通过比较吸引的范德华力和由这些效应产生的力,就可以预测不同清洗过程的内在能力和局限性,特别是对于下一代集成电路必须考虑的细粒子。三种粒子去除过程,即通用过程能够去除所有颗粒大小和类型甚至图案晶圆,过程呈现相同的理论能力但实际上受限于粒子的可及性,最后清除不能去除所有的颗粒大小。