
扫码添加微信,获取更多半导体相关资料
在半导体器件的制造过程中,兆声波已经被广泛用于从硅晶片上去除污染物颗粒。在这个过程中,平面硅片被浸入水基溶液中,并受到频率在600千赫-1兆赫范围内的声能束的作用。声波通常沿着平行于晶片/流体界面的方向传播。兆频超声波清洗领域的大部分工作都是针对寻找兆频超声波功率和磁场持续时间等条件来优化粒子去除。已知或相信在兆电子领域中有几个过程是有效的,即微空化、声流和压力诱导的化学效应。兆声波可以想象为以音速传播到流体中的压力变化。当声波通过固体颗粒时,该波中的压力梯度会对该颗粒施加作用力。
本文的主要目的是从理论上研究与二阶声场相关的现象,如声波流动,特别是兆频超声波清洗过程中颗粒去除的施里希廷流动。该理论研究由两部分组成,即计算固体/粘性流体界面处的时间相关(一阶)声位移场,然后计算时间无关(二阶)压力场。
在典型的兆频超声波清洗槽中,一次清洗几个晶片。晶片在盒子中彼此平行排列。兆声波传播通过的介质是不均匀的,因此可以简单地表示为由水基流体层分开的交替硅板组成的层状复合材料。因为晶片直径明显大于兆声波的波长,所以层状复合材料在这里被视为在平行于晶片/流体界面的方向上是无限的。
此外,为了简化模型,我们将固体介质视为各向同性的。在本文中,我们考虑两种多层几何形状。首先,我们研究了入射声波和由硅和水组成的两个半无限同质介质之间的单个界面之间的相互作用。这个系统将被称为硅/水系统。这个简单的界面用来建立计算二阶声场的数学过程。然后处理对应于浸入水中的一个晶片的更真实的几何形状。这个有两个平行界面的系统被模拟成一个固体硅板,将两个半无限的水介质分开。由于硅晶片的半径远远超过它的厚度,所以它被认为是无限长的。我们将该系统称为水/硅/水系统。
图1说明了本文研究的分层复合系统的类型。所有界面都选择为垂直于笛卡尔坐标系(X1,X2,X3)的X3轴。
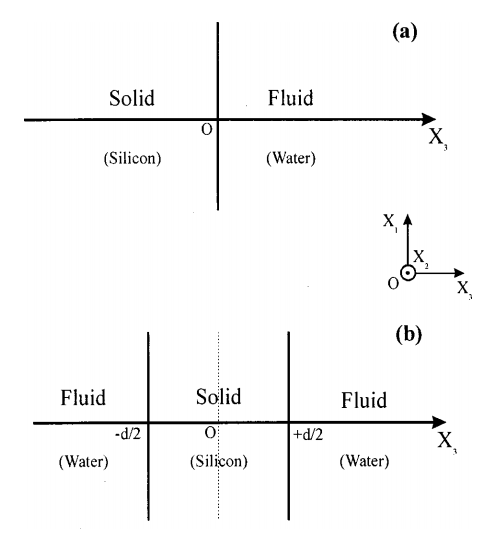
图1 所研究的两个非均匀系统的说明,a硅/水系统和 b水、硅水系统
我们通过厚度为d的固体介质1的平板模拟硅晶片,其表面垂直于X3轴,位于X3 = d/2[见图1(b)]。硅板的两侧耦合到两个半无限介质。半无限介质由水(介质2)构成,浸入水中的硅板的格林函数的倒数,定义在固体/流体界面,然后从方程得到。这种非均匀介质的振动态密度的变化由方程1用数值方法确定。使用无限水介质作为参考系统,我们取一个厚度为d=0.64 mm的硅片作为标准晶片的代表,声速和粘性系数与秒相同。图6报告了在单一固/水界面情况下使用的相同实k的状态密度随脉动的变化。

图6 对于由浸在水中的硅板(晶片)组成的系统,振动状态密度的变化是脉动的函数
Mrad/s附近的特征也是流体体积带的下限。由于平板沿X3轴具有有限的尺寸,固体的体带没有出现在该图中。有限平板仅具有离散的振动状态,当耦合到半无限流体介质时,这些振动状态变成共振状态。共振态表现为流体体带内态密度的尖峰。我们注意到这些共振发生时的脉动与硅的横向和纵向体带的下限相对应。最后,δn在0.33 MHz左右的ω水体带下限以下呈现出一个清晰的峰值。该峰值与板振动的第一弯曲模式相关。由于高阶弯曲模式的频率超过了本方法中考虑的频率,因此未观察到高阶弯曲模式。一阶弯曲模式位于硅晶片/水界面附近的流体中。
在图11中,我们报告了由于固体/流体界面处的瑞利波、水中晶片的体波以及范德瓦尔斯粘合力引起的移除力随粒子半径的变化。与瑞利波和体波相关的移除力在超过几微米的半径处穿过粘合力。因此,二阶流动力F3仅能够从硅晶片上去除大的污染物颗粒。然而,对于小颗粒来说,粘附力占主导地位,并且去除的分量足以去除颗粒。然而,我们注意到,沿着固体/流体界面的流动力是几个数量级的。然后,该流动力可以用作通过沿着晶片表面滚动和牵引颗粒来清洁晶片的机制。当污染物颗粒到达晶片边缘时,它们将从晶片表面去除。污染物颗粒沿晶片的运动方向由F1的符号确定。
我们计算了硅和水的单一界面情况下的一阶声场浸入水中的硅板。固体被视为各向同性弹性介质,水被视为粘性流体。然后使用一阶声场来确定二阶流动力,这使得我们能够估计作用在球形污染物颗粒上的去除力粘附在固体表面上。然后将去除力与二氧化硅颗粒和水中平坦硅表面之间的范德华粘附力进行比较。我们发现,一般来说,第二次有序声场太小,无法去除亚微米颗粒。然而,平行于固体/流体界面F1的流动力的分量是数量级的。在这种情况下,f1可能导致建议的一些作者通过滚动和拖拽机制去除颗粒。关于巨气清洗,习惯是将沿硅/水界面作用在污染物颗粒上的力与粘附力进行比较。这种做法并没有反映这两种力相互垂直的事实。
对粒子在平行于硅/水界面的方向上的运动没有阻力,但在粒子/硅界面上有摩擦力。由于流力F1,流体向X1方向流动将导致阻力,可以根据摩擦力的大小推动污染物粒子或滚动它。对这一机制的详细研究将是后续发表的主题。
最后,我们已经证明,像传统上在巨硅清洗罐中那样,对硅片进行放牧入射声波可能不会导致最佳的清洗效率。事实上,我们已经证明了流力的正常分量和平行分量强烈地依赖于入射波的入射角。我们的结果表明,通过将晶圆进行入射角范围的入射声波采样,可以提高清洗效率。